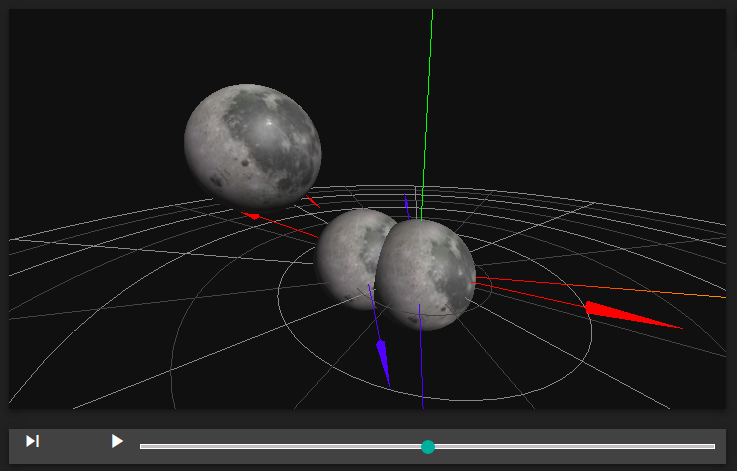
3D gravity sim

In this project, I basically applied what I learned about classical physics in 12th grade to simulate gravitational interactions between ponctual objects in 3d.

I worked on it during the first lockdown, with 2 of my classmates, at a time when we had no idea what differential equations were.

It’s mostly a js project, we used Three.js as 3d engine and materialize as html/css framework.

Currently it’s really shitty, and there’s a high probability it will stay unfinished forever. But you can test it online if you really want to.

How does it work ?

As I’m writing this, it’s been one year since I stopped working on this project. It’s the right time to dive one last time in the old messy code, and see what I can learn from the not-so-wise design choices we made when working on the project.

Basically, for each new frame, the code compute the acceleration of each point, according to Newtown’s second law : \(\sum \vec{F} = m \vec{a}\)

Then it updates each point’s position and velocity according to :

\[\vec{v_{t+1}} = \vec{v_t} + \Delta T \vec{a}\] \[\vec{p_{t+1}} = \vec{p_t} + \Delta T \vec{v_t}\]

I don’t understand why we absolutely wanted to create our simulator in 3d. Clearly, a third dimension doesn’t add a lot of new things, beside some more difficulty with the 3d viz part of the project (which mostly consisted in reading threejs documentation… not really passionating).

The weirdest thing with our code was that the actual simulation is computed in real time inside the animation loop of threejs. This doesn’t really makes sense because we didn’t plan to let the user interact with the 3d objects during the simulations. Also, just simulating before playing the animation wouldn’t have been a big problem as just keeping track of the positions of the 3d objects would have been quite lightweight.

The way we approached is problematic because, currently, you can’t reduce the time step \(\Delta t\) to get more precise results without reducing the speed at which the animation is playing.